
|

|

|
|
The Three Sided SquareI am told that if you go 10,000 miles in a straight line, turn 90 degrees to the right, go 10,000 more miles , turn 90 degrees again, and go 10,000 miles, you will end up where you started.Let's find out if this is true. In the diagram at right, we started at the North pole, then went a quarter of the way around the globe, or about 6,200 miles ( 1, 2, 3 - orange lines ). And look at that! After walking only 3 sides of a square, we get back to where we started. Let's try again, with the purple triangle, 4 5 6. This time we only walk 2,000 miles. Straight South from the North Pole, if (success){ turn exactly 90 degrees and we're walking East along a latitude line. 90 degrees more and we walk due North to where we started. |
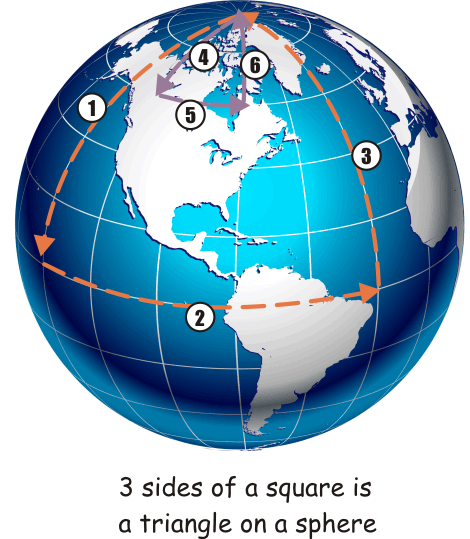
|
In fact, this phenomenon is independent of distance traveled. It works just the same if you go 1,000 miles, or only one mile.
|
Also, as the earth is round, the coordinate system can be moved to originate anywhere, in this case, Hawaii (ish). As before, you can see easily that triangle 1, 2, 3 brings you back to Hawaii. Direction is unimportant as seen in triangle A, B, C. The length of C is also unimportant. As long as A and B are the same length and you always turn exactly 90 degrees, you will return to your starting point. So you too can now easily prove that the earth is round. Just drive one mile in any direction. turn left, drive one mile, turn left again and drive the third mile. When you see that you are right back where you started, you can put an end to this flat earth nonsense once and for all. |
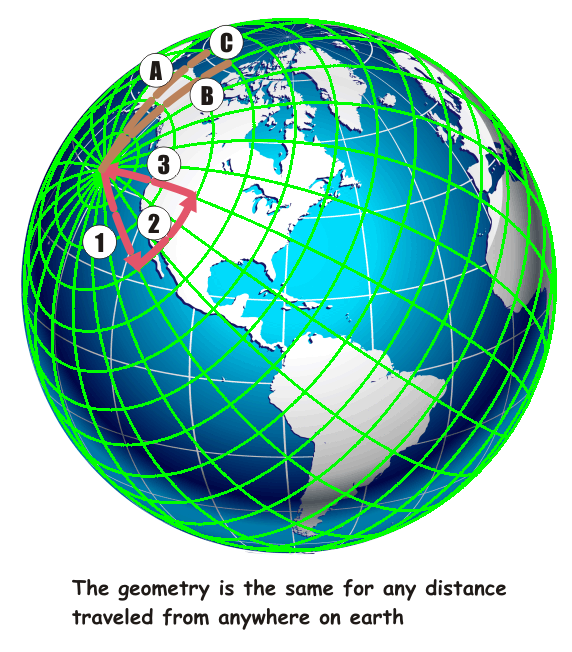
|

|
|
|
|
|
|
|
|
|